Warning

The content was translated from the Chinese version by Generative AI. Please double-check the content.

Original Problem Description

The Monty Hall problem can be described as follows: In this TV show, there are three doors, and exactly one of them has a car behind it.

The audience randomly selects a door. After the contestant makes their choice, the host does not open that door immediately; instead, the host opens one of the remaining two doors that has no car behind it.

Subsequently, the host offers the audience a chance to switch their choice: the audience can either keep their initial choice or switch to the other unopened door.

Question: Which choice gives a higher probability of winning the car: switching doors or not switching?

(Description adapted from 知乎)

First, the answer: Switching gives a higher probability, $\frac{2}{3}$; not switching gives only $\frac{1}{3}$.

Python Experiment

Facts speak louder than words. We can simulate the scenario using Python:

import random

def which_choice_can_earn_car():
    # Initialize three doors
    doors = [1, 2, 3]
    # Randomly select one door to hide the car
    car = random.choice(doors)
    # Randomly select one door as the audience's initial choice
    choice = random.choice(doors)

    # Doors the host can open (excluding the audience's choice and the car door)
    doors_can_be_opened_by_host = [i for i in doors if i not in [car, choice]]
    # Host randomly chooses a door to open from the available ones
    door_opened_by_host = random.choice(doors_can_be_opened_by_host)

    # Assume the audience switches doors; the new choice is the only remaining door after removing the initial choice and the host's opened door
    doors.remove(door_opened_by_host)
    doors.remove(choice)
    re_choice = doors[0]

    # Since the host always opens a door without the car, the car must be behind one of the two doors chosen by the audience. We directly check these two to determine if switching is better.
    if choice == car:
        return 'No change'
    elif re_choice == car:
        return 'Change'

if __name__ == '__main__':
    # Count the number of wins for switching and not switching
    change = 0
    no_change = 0
    # Test 10,000 times
    for i in range(10000):
        result = which_choice_can_earn_car()
        if result == 'Change':
            change += 1
        else:
            no_change += 1
    # Output results
    print(f'Change: {change}\nNo change: {no_change}')

On the first run, the magical random library was kind enough to output the theoretical probability directly:

Change: 6667
No change: 3333

Thus, it is clear that switching gives a probability of $\frac{2}{3}$, while not switching remains $\frac{1}{3}$ (I don’t need to explain that the winning probability without the host opening any door is $\frac{1}{3}$, right?).

Simple Analytical Proof

Thanks to the excellent foundation of nine-year compulsory education, we can all agree on the following conclusions:

1. During program execution, observing the program (e.g., outputting more intermediate steps) does not affect the result.
2. The probability of initially choosing the car (i.e., winning without the host opening any door) is $\frac{1}{3}$.
3. The probability that the car is behind one of the two doors not initially chosen is $\frac{2}{3}$.
4. After the host opens a door, the winning probability of switching cannot be $\frac{1}{3}$.

(The first point means computer programs do not follow the quantum mechanical uncertainty principle—this non-rigorous explanation is for simplicity.)

With conclusion 4 established, we only need to explain why switching gives $\frac{2}{3}$ instead of $\frac{1}{2}$.

From a Programming Perspective

Modify the code as follows:

    # Initialize three doors
    doors = [1, 2, 3]
    # Randomly select one door to hide the car
    car = random.choice(doors)
    # Randomly select one door as the audience's initial choice
    choice = random.choice(doors)

Add an output statement to check if the initial choice wins:

    # Initialize three doors
    doors = [1, 2, 3]
    # Randomly select one door to hide the car
    car = random.choice(doors)
    # Randomly select one door as the audience's initial choice
    choice = random.choice(doors)

    print(choice == car)

Obviously, the probability of outputting True here is $\frac{1}{3}$ (conclusion 2).

Since the values of car and choice do not change, this probability remains the same whether checked here or at the end of which_choice_can_earn_car.

By the end of the function, the host has eliminated a door without the car, so the car must be behind either the initial choice or the switched choice. The switched choice is uniquely determined after the initial selection and host’s door opening. Thus, the winning probability of switching equals the probability of initially not winning, i.e., $1 - \frac{1}{3} = \frac{2}{3}$.

From an Intuitive Perspective

The initial winning probability is $\frac{1}{3}$, and the probability of not winning is $\frac{2}{3}$.

Regard the two unchosen doors as a single group, which has a combined winning probability of $\frac{2}{3}$. Initially, we cannot use this group directly since it contains two doors, each with $\frac{1}{3}$ probability.

However, when the host opens one non-winning door from this group, we can now utilize the full $\frac{2}{3}$ probability by choosing the remaining door in the group. Since局部 operations within the group do not affect its total probability, and the group now has only one door left, that door inherits the entire $\frac{2}{3}$ probability.

For Extra Conviction

Scale up to 10,000 doors.

Suppose there are 10,000 doors with one car. You randomly choose one, and the host opens 9,998 non-winning doors, leaving one unopened door besides your initial choice.

Would you switch to win the car? Most people would switch, as the initial winning probability is $\frac{1}{10000}$. If you initially lost (probability $\frac{9999}{10000}$), switching guarantees a win. Thus, switching gives $1 - \frac{1}{10000} = \frac{9999}{10000}$ probability.

The logic is identical when scaling down to 3 doors.

From a Simple Tree Diagram

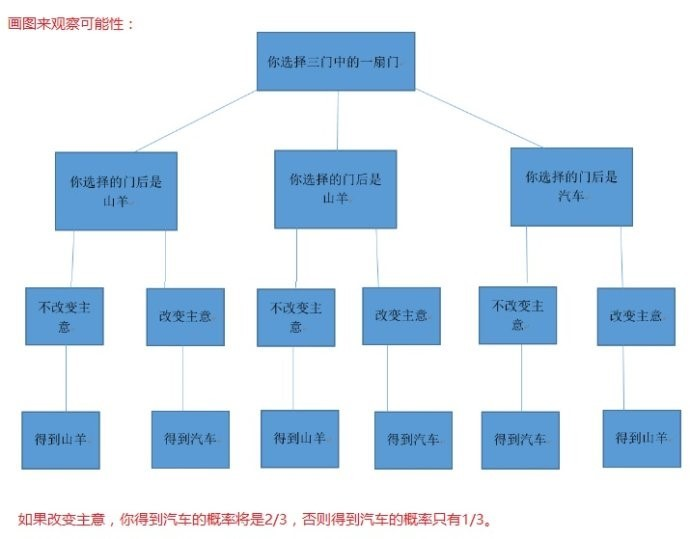
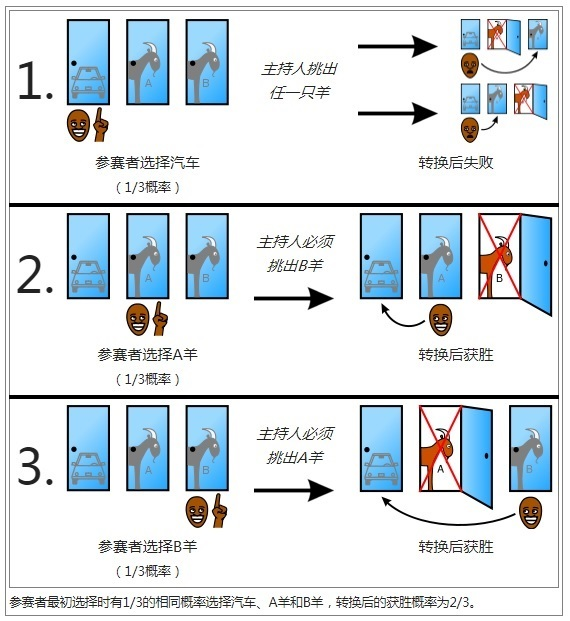
Image source: https://blog.csdn.net/weixin_42467709/article/details/82882617

Copyright

License under:Attribution-NonCommercial-ShareAlike 4.0 International (CC-BY-NC-SA-4.0)