题目描述

给出两个字符串 $s_1$ 和 $s_2$，若 $s_1$ 的区间 $[l, r]$ 子串与 $s_2$ 完全相同，则称 $s_2$ 在 $s_1$ 中出现了，其出现位置为 $l$。 现在请你求出 $s_2$ 在 $s_1$ 中所有出现的位置。

定义一个字符串 $s$ 的 border 为 $s$ 的一个非 $s$ 本身的子串 $t$，满足 $t$ 既是 $s$ 的前缀，又是 $s$ 的后缀。 对于 $s_2$，你还需要求出对于其每个前缀 $s'$ 的最长 border $t'$ 的长度。

输入格式

第一行为一个字符串，即为 $s_1$。

第二行为一个字符串，即为 $s_2$。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 $s_2$ 在 $s_1$ 中出现的位置。

最后一行输出 $|s_2|$ 个整数，第 $i$ 个整数表示 $s_2$ 的长度为 $i$ 的前缀的最长 border 长度。

输入输出样例

In 1：

ABABABC
ABA

Out 1：

1
3
0 0 1

样例解释：

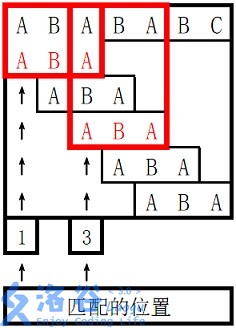
对于 $s_2$ 长度为 $3$ 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 $1$。

数据范围

对于全部的测试点，保证 $1 \leq |s_1|,|s_2| \leq 10^6$，$s_1, s_2$ 中均只含大写英文字母。

题解

如题所述，这就是一道纯粹的模板题。不要被输出说明的第二句吓到，他其实就是让你输出会跳指针罢了。

下面我们来讲解KMP算法。

首先假设我们要在字符串 ①ABAABABACB 中匹配 ②ABABA

最简单的暴力方法，分别从①的第一位，第二位，第三位……开始截取长度和②相等的字符串，逐字符判断该产生的字符串和②是否一样。

画图表示如下：

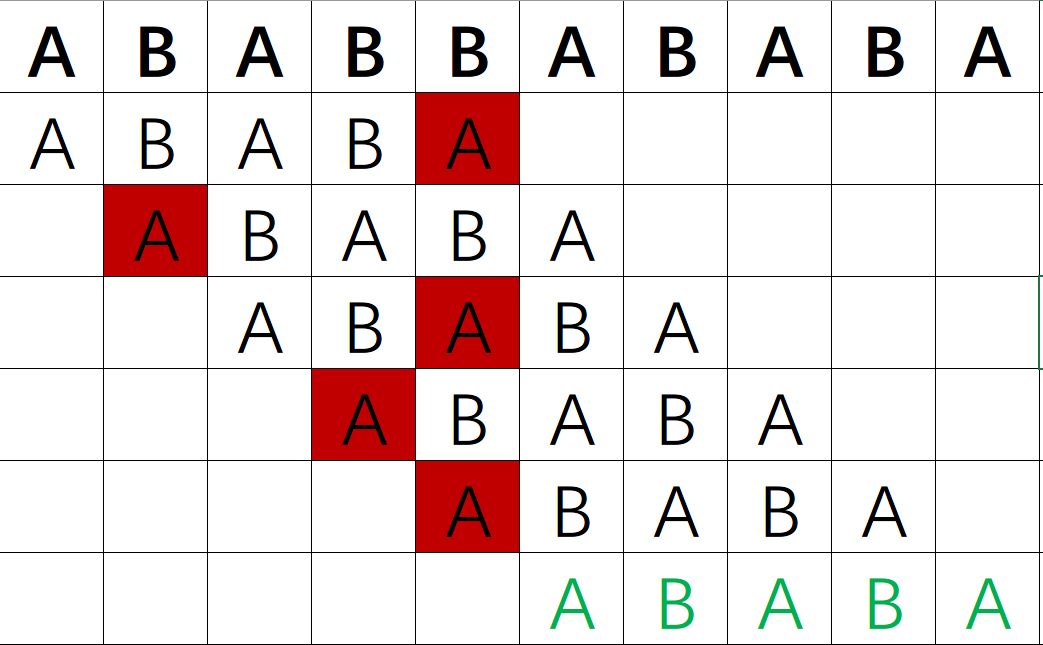
想必这个方法大家都会吧，复杂度近似 $O(nm)$ 也易得。

现在让我们来注意这两次尝试

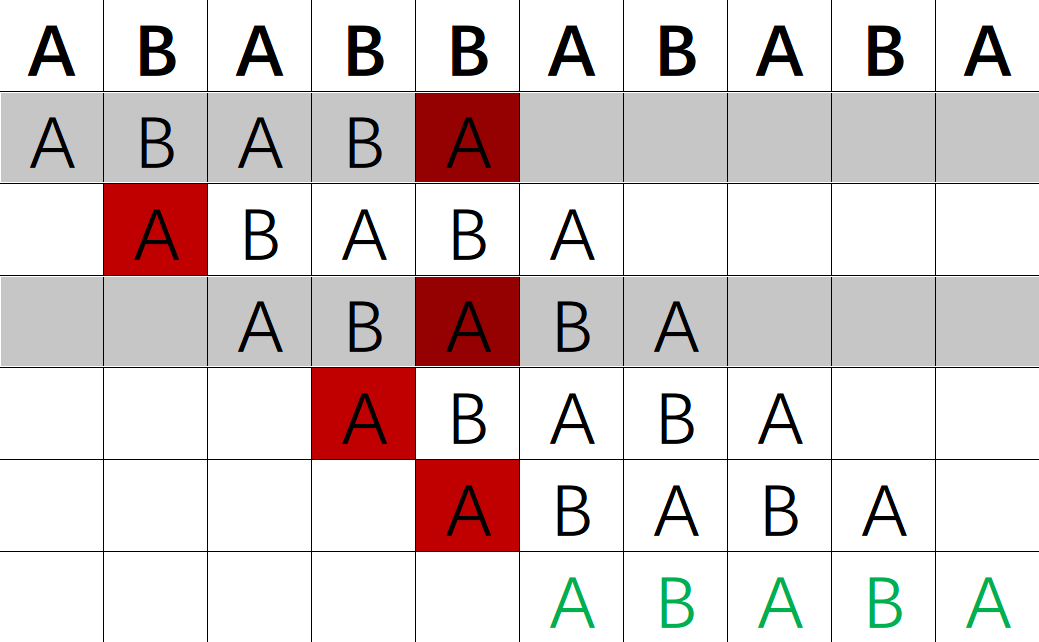
（为方便描述，第一行加粗的为原串，往下的六行分别为模式串的第 $i$ 次匹配）

如果人脑模拟到第 $1$ 次匹配的位置，我们会发现前四个能够正常匹配的字符中，有两个重复的 AB ，那么顺理成章把前两个 AB 放到后两个 AB 的位置即可（也就是直接跳到第 $3$ 次匹配的状态）。每次都这么做，效率显然可以大大提高。

也就是说，我们每次出现匹配失败的位置后，模式串不非得直接去匹配原串的下一个字符，而可以直接多跳一些。这就是KMP算法的核心。

那么我们怎么找每次跳多少个呢？

如果我们在模式串的 $q$ 位置和原串的 $p$ 位置尝试匹配时失配了，那么就看看模式串从第 $1$ 位到第 $q - 1$ 位的字符构成的字符串 前缀 和 后缀 最大的相同长度。注意，这里的前缀和后缀长度都不能等于原串。我们称这个“最大的相同长度”为最大公共元素长度。显然，当模式串的 $q$ 位置失配，我把模式串能与它本身 $[q-1-z, q-1]$ 这个区间内的字符匹配的 $[1,z]$ 部分放过来到 $p$ 以前，那么就可以在不让 $p$ 回溯的情况下继续去求解了。

我承认自己语文不好，放张图理解。由于这里有一张很清晰的图片，我就不再重复工作了。图片中是对一个值为 ABCDABD 的模式串做分析。

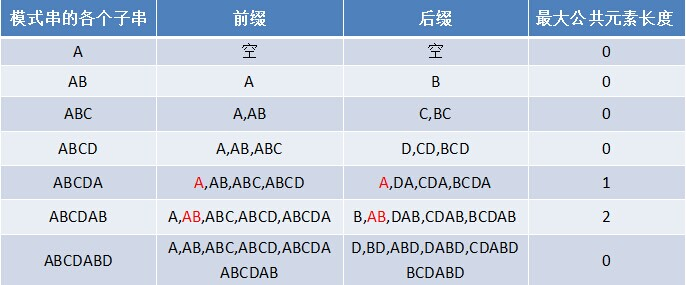
图片来源：从头到尾彻底理解KMP（2014年8月22日版）_v_JULY_v的博客-CSDN博客_串的next数组怎么求。说句题外话，这个博主写的是我目前发现的全网描述最细致的了，我也是最开始看这个理解的，看我的语言风格搞不懂的同学们可以去换个口味。

那么对于本文的模式串 ABABA ，求解的结果应该是这样子的

让我们回到这张图：

显然当第 $1$ 次匹配失配时，我们已经尝试了 $4$ 个字符，对应的模式串最大公共元素长度为 $2$ ，所以我们可以直接把模式串向后移动 $2$ 位，而不是仅仅 $1$ 位。

得出结论：失配时，模式串向右移动的位数为 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值

回到原题，我们的AC代码如下：

#include <cstring>
#include <iostream>
const int MAXN = 1000010;
using namespace std;
int kmp[MAXN];
char a[MAXN], b[MAXN];
int main() {
    cin >> a + 1 >> b + 1;  // 从第一位开始输入，个人习惯而已不必纠结
    int la = strlen(a + 1), lb = strlen(b + 1);  // 求长度
    for (int i = 2, j = 0; i <= lb; i++) {
        // 构建kmp数组，即计算最大公共元素长度
        while (j > 0 && b[i] != b[j + 1]) j = kmp[j];
        if (b[j + 1] == b[i]) j++;
        kmp[i] = j;
    }
    for (int i = 1, j = 0; i <= la; i++) {
        // 真正的匹配过程
        while (j > 0 && b[j + 1] != a[i]) j = kmp[j];
        if (b[j + 1] == a[i]) j++;
        if (j == lb) {
            cout << i - lb + 1 << endl;
            j = kmp[j];
        }
    }

    for (int i = 1; i <= lb; i++) cout << kmp[i] << " ";  // 打印kmp数组
}

毕竟在代码里，我们是无法移动字符串的，那我们能做什么呢？

——构建指针，移动指针。

先看匹配过程。$i$ 是表示目前正在匹配原串的第 $i$ 位，$j$ 表示正在用模式串的第 $j$ 位与之匹配。b[j + 1] != a[i] 表示当前状态已经失配，需要将模式串右移，也就是将模式串指针左移。模式串右移的长度是 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值 ，那么指针左移的长度就是 已匹配字符数 - (已匹配字符数 - 失配字符的上一位字符所对应的最大长度值) ，也就是 失配字符的上一位字符所对应的最大长度值 。

那么为啥 $j>0$ 呢？你可以暂且理解为特判——如果 $j$ 已经等于 $0$ 了还不跳出不就死循环了嘛……

b[j + 1] == a[i] ，j++ 好理解是要继续匹配模式串下一位，而这个条件判断则有两种情况。当 $j$ 仍大于 $0$ 时，那么该条件一定满足（否则无法跳出while）；当 $j$ 已经减小到 $0$ 时，那么就真的需要好好看看能不能开始下一次匹配了。不行？那就让 i++ 之后再开始匹配。

j == lb ，代表模式串被匹配完了，那么我们就输出这个匹配位置的起始坐标，不用再说了。

最后，kmp数组，也就是最大公共元素长度，我们是如何求得的？

看代码

一定要仔细看

有没有发现

其实和匹配过程一模一样，只不过这里是用部分模式串去匹配整个模式串。

我们很容易发现在上面的匹配过程中，任何一次for循环结束时，原串的第 $i$ 个字符和模式串的第 $j$ 个字符都是一样的，除非 $j$ 等于 $0$ 。而构建kmp数组的过程中指针 $i$ 从 $2$ 开始，可以保证匹配到的不会是从模式串头部开始的一模一样的区间。那么：

• 当 $j$ 不等于 $0$ ，此时模式串前 $j$ 位与后 $i-j$ 位匹配，求得此时对应的最大公共元素长度为 $j$
• 当 $j$ 等于 $0$ ……嗯……那就是没匹配上，最大公共元素长度为 $0$ 呗，合情合理

结束。

思考一个问题：上文已经很清晰说明了KMP算法求得的解一定正确，但是有没有漏解的情况？

要凌晨三点了，太困了，关于正确性的证明先鸽了，大家可以看看这篇文章，写的真的很好，我要补充大概也是从他这里拿思路哈哈哈哈：反证法证明：为什么KMP算法不会跳过（漏掉）正确的答案_马小超i的博客-CSDN博客_kmp算法为什么不会漏解

版权所有

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)