三门问题的 Python 实验数据 & 直观但非严谨的证明
原题描述
三门问题的主要内容表述如下：在这个电视节目中有三扇门，其中有且仅有一扇门后面放有汽车。
此时观众要随机选择一扇门，在参赛者选择了一扇门之后，主持人并不会立刻打开这扇门，而是从剩下的两扇门中打开一扇没有汽车的门。
随后主持人会给观众提供一次重新选择门的机会，此时观众可以保持自己的第一选择不变，也可以更换自己的选择选择另外一扇未被开启的门。
问：此时换门与不换，哪种选择选中汽车的概率更大？
（描述复制自三门问题 - 知乎，有删改）
先说答案：换门后概率更大，为 ；不换的话只有 。
Python 实验
事实大于雄辩，我们可以使用 Python 对实际情况进行模拟：
import random
def which_choice_can_earn_car():
# 初始化三扇门
doors = [1, 2, 3]
# 随机选择一扇门为有车的门
car = random.choice(doors)
# 随机选择一扇门为观众选择的门
choice = random.choice(doors)
# 可以被主持人开的门（不包括观众选择的门和有车的门）
doors_can_be_opened_by_host = [i for i in doors if i not in [car, choice]]
# 主持人在可开的门中随机选择的门
door_opened_by_host = random.choice(doors_can_be_opened_by_host)
# 假设观众更换门，则更换后的门一定是除去“第一次选择的门”和“主持人开的门”后剩下的唯一一个
doors.remove(door_opened_by_host)
doors.remove(choice)
re_choice = doors[0]
# 由于主持人打开的一定是没有车的门，因此车一定在观众两次选择的门之一中，直接判断这两个门后面是否有车，即可知道是否应该换
if choice == car:
return 'No change'
elif re_choice == car:
return 'Change'
if __name__ == '__main__':
# 统计换门中奖和不换门中奖的次数
change = 0
no_change = 0
# 测试一万次
for i in range(10000):
if which_choice_can_earn_car() == 'Change':
change += 1
else:
no_change += 1
# 输出结果
print(f'Change: {change}\nNo change: {no_change}')第一次运行，神奇的 random 库就很给我面子，直接输出了理论概率：
Change: 6667
No change: 3333由此可见，的确换门的概率为 ，不换门的概率依然是 （主持人不开任何门的中奖概率是 不用我再说了吧）
简单的分析证明
相信凭借九年义务教育的优秀成果，大家都认可这样下面这些结论：
- 在这段代码运行过程中，对程序进行观测（例如输出更多中间的运算步骤）不影响运算结果
- 第一次选中车的概率（即主持人不开门、直接在观众第一次选择后公布答案的情况下选中汽车的概率）为
- 车在第一次选的门之外的两个门中的任意一个的概率为
- 当主持人打开一扇门后，观众换为剩下的最后一扇门后，中奖的概率一定不是
（第一条也就是说，计算机程序运行不适用量子力学测不准原理，为了通俗易懂做前面的非严谨解释）
有了上面的结论 4 就好说了，我们现在只需要说明为什么换门后概率是 而不是
从程序角度出发
我们将这段代码进行更改：
# 初始化三扇门
doors = [1, 2, 3]
# 随机选择一扇门为有车的门
car = random.choice(doors)
# 随机选择一扇门为观众选择的门
choice = random.choice(doors)在最后增加一行输出语句，判断观众第一次的选择能否得到汽车：
# 初始化三扇门
doors = [1, 2, 3]
# 随机选择一扇门为有车的门
car = random.choice(doors)
# 随机选择一扇门为观众选择的门
choice = random.choice(doors)
print(choice == car)显然在此处输出为 True 的概率为 （结论2）
又由于变量 car 和 choice 的值均未发生变化，所以无论是在此处还是 which_choice_can_earn_car 函数的最后，这个判断语句答案为 True 的概率都不会发生变化
又因为在函数最后，主持人已经排除了一个没有车的门，所以车只有可能在第一次选的门和第二次选的门中的一个，而第二次选的门在观众第一次选完、且主持人打开一扇门后是唯一确定的，所以换选选中汽车的概率就是不换选未选中汽车的概率，即 。
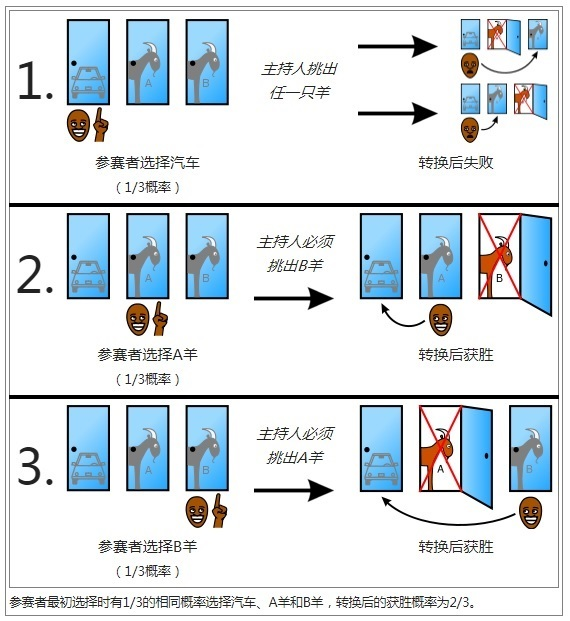
从直觉角度出发
最开始选中的概率是 ，选不中的概率为 。
我们可以把未选择的这两扇门看作一个整体，这个整体的中奖概率就是 。但是此时我们无法直接利用这个整体的概率，因为这里面还有两扇门，选择这个整体中的任意一扇结果仍是 。
而主持人在这个整体的两扇门中打开了一扇没有汽车的门，此时我们选择这个整体便可以利用整个 啦！因为看作整体后，局部的操作不会影响这个整体的概率，而此时整体中的选项从两个变成了一个，自然这一个就分配到了全部 的概率。
再有说服力一点
我们把三扇门放大到一万扇门。
假设现在有一万扇门，一扇门后面有汽车。现在你随机选择一个，主持人打开了 9998 扇后面没有汽车的门，现在除了你选择的还剩下一个。
此时为了选中汽车，你换不换？相信大多数人的选择是换，并且你很容易接受，最开始我们选中的概率仅有万分之一，而如果我们第一个没选中，那么换门后一定选中，也就是说换门后的概率是 。
那么把 10000 换成 3，道理其实是一样的。
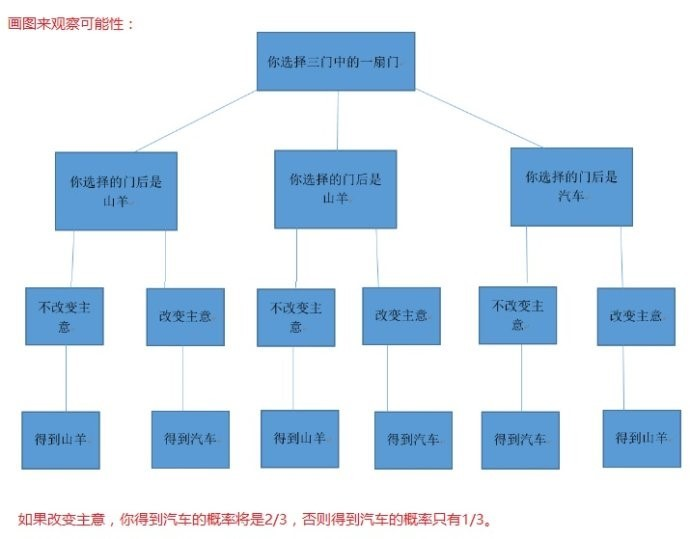
最朴素的树状图角度理解
