题目描述

严先生是华中科技大学的大一新生。

体育选课了，严先生作为幸运 Ex 的联创人才，选上了“户外运动”这门课。

严先生第一次课的内容是“定向越野”，具体来说是这样的：校园内共有 $n$ 个检查点，他们之间有 $n − 1$ 条路径相连。换句话说，检查点之间构成了一棵树。

为了让事情更有趣一点，严先生把这些检查点划分为两种，权值分别为 $0$ 和 $1$。但是学校有打卡规定，在一次越野之后，经过的所有检查点的权值异或和必须为 0。

严先生的越野方案是这样的: 从某一个检查点开始, 不经过重复的检查点, 随机的选择一个与当前检查点有路径相连的检查点, 直到走到无路可走, 这算完成一次定向越野。

但是严先生是联创团队 lab 组的优秀人才, 严先生可以随意钦点每一个检查点的权值。

也就是说, 严先生会让每一个点轮流做一次根节点, 你需要让根节点到每一个叶子节点的路径权值异或和都为 $0$, 这就是一个合法的方案。

现在严先生想知道, 总共有多少种合法的方案。输出结果对 $1000000007$ 取模。

输入格式

第一行一个整数 $n$ ，表示检查点的数量。

第二行开始每行两个整数 $u, v$ ，表示检查点 $u$ 和检查点 $v$ 有无向的路径相连

输出格式

一行一个整数，表示对 $1000000007$ 取模后的答案

输入输出样例

In 1：

3
1 2
2 3

Out 1：

10

In 2：

6
1 2
2 3
1 4
4 5
5 6

Out 2：

128

数据范围

对于 $20\%$ 的数据，$1 ≤ n ≤ 10$

对于 $40\%$ 的数据，$1 ≤ n ≤ 1000$

对于额外 $20\%$ 的数据，检查点的链接将会成为一条链。

对于 $100\%$ 的数据，$1 ≤ n ≤ 10^6$

---

模拟拿20，相信大家都会。这道题想拿全分事实上需要给结论。

先给出代码，想起来或者有人点赞评论的话再来补说明

我们先来画一棵树

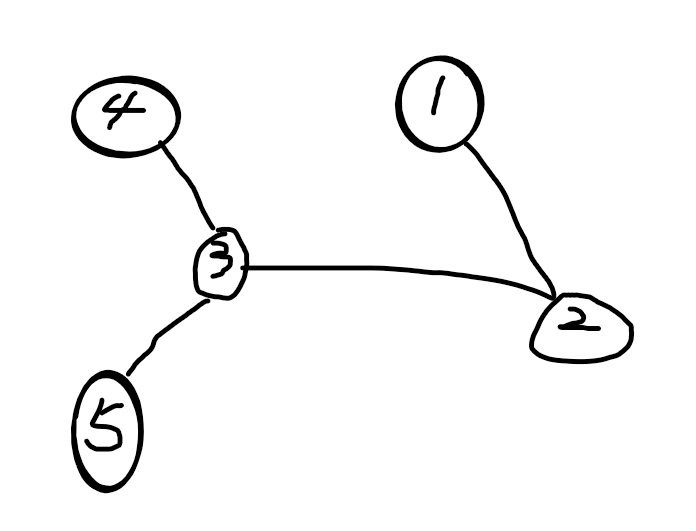
任选一条路径，比如这里我用1-2-3-4，可以理解1 2 3三个点取任意值的时候，只要最后一个结点4只要对应前三个点的异或值选择0或1，则可以控制四个点的异或和。

因此现在有两种情况（n为节点总数，cnt是中间节点即非叶节点的总个数）：

1. 作为根的是某个中间节点，则可能性总数为 $2^{cnt} \times cnt$ （每个非叶节点做根的可能性数量*非叶节点的个数）
2. 作为根的是某个叶子节点则，可能性总数为 $2^{cnt+1} \times (n-cnt) = 2^{cnt} \times (n-cnt) \times 2$ （每个非叶节点做根的可能性数量*非叶节点的个数）。这里比上一情况指数增加1是因为根节点本身也可以变但是没有记在cnt里面。

为什么会不一样呢？因为不同节点做根时形成的树中可作为路径末尾节点的点的数量会发生变化

#include <bits/stdc++.h>
using namespace std;

int n, cnt, a[1000001];

const int mod = 1000000007;

int main() {
    cin >> n;
    for (int i = 1; i < n; i++) {
        int x, y;
        cin >> x >> y;
        a[x]++;
        a[y]++;
    }
    for (int i = 1; i <= n; i++)
        if (a[i] > 1) cnt++;
    long long ans = 1;
    for (int i = 1; i <= cnt; i++) ans = (ans << 1) % mod;
    cout << (ans * (cnt + (n - cnt) * 2) % mod) % mod;
}

版权所有

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)