P / NP 复杂度问题
2025-10-07
P 问题(Polynomial Problem)
P 是在复杂度类问题中可于确定型图灵机以多项式量级(或称多项式时间)求解的决定性问题。
决定性问题
输出只有“是”或“否”的问题。
换句话说,P 是指可以通过复杂度为 O(nk) 的算法解决的问题(其中 k 为常数)。
举个简单的例子,查找一个长度为 n 的列表中是否存在元素 m 就是一个 P 问题,该例中朴素算法的复杂度为 O(n)
NP 问题(Nondeterministic Polynomial Problem)
NP 问题包含可在多项式时间内验证其解是否正确,但不保证能在多项式时间内能找出解的决定性问题。
这个问题的例子如下:给定一个有 n 个整数的集合 S,问是否存在一个 S 的非空子集 S0,使得 S0 中所有元素相加的结果为 0 ?
对于这一个问题:
- 不保证能在多项式时间内求解:枚举的时间复杂度为 O(2n)
- 可在多项式时间内验证其解是否正确:对于任意一个子集,执行一次复杂度不超过 O(n) 的累加即可验证该子集是否符合条件
P = NP 问题
即便根据上方的定义,大部分人的直觉都是 P 问题是 NP 问题的子集。然而也有科学家认为,P 问题和 NP 问题本质上是相同的。
简单来说,P = NP 即:若问题的答案可以在多项式时间内验证,其答案是否也可以在多项式时间内被计算出来。
NP-complete 和 NP-hard
在看这两个概念之前,我们先来了解一下 P、NP、NP-complete 和 NP-hard 之间的关系。根据命题 P = NP 的成立与否,我们可以画出如下左右两种关系图(请重点关注左侧部分):
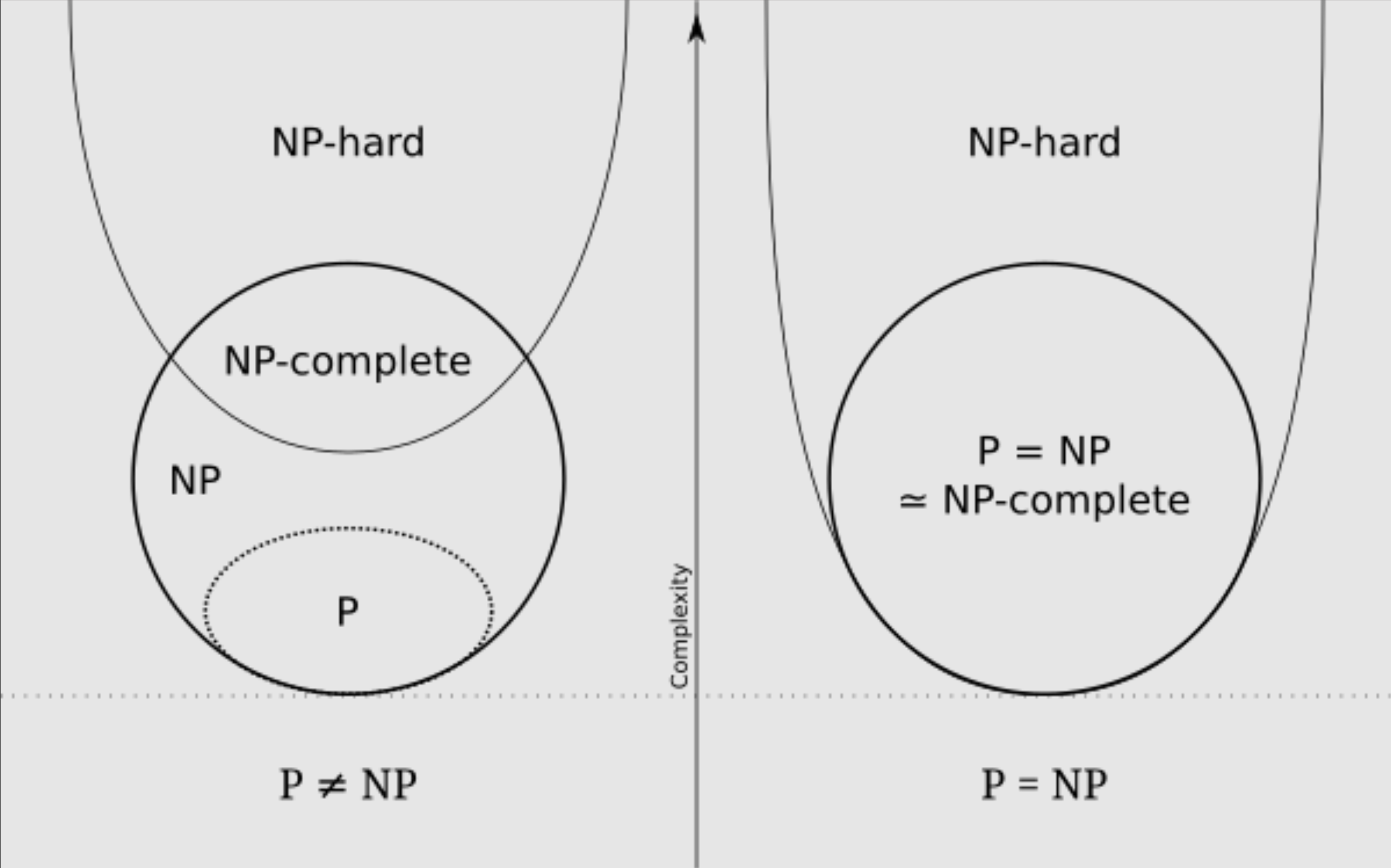
NP-complete
又称 NP 完全或 NP 完备。NP- complete 是 NP 中最难的决定性问题,所有 NP 问题都可以在多项式时间内被归约为 NP 完全问题。
归约
将某个计算问题变换为另一个问题的过程。针对两个问题 A 和 B ,如果存在一个 O(nk) 时间的(决定性)算法,将每一个问题 A 的输入转换成问题 B 的输入,使得问题 A 有解时,当且仅当,问题 B 有解。
NP-complete 是 NP 和 NP-hard 的交集。
NP-hard
如果所有 NP 问题都可以多项式时间归约到某个问题,则称该问题为 NP 困难。
特别说明的是,与 P 和 NP 的定义不同,NP-hard 的定义不要求该问题是一个决定性问题。
NP-hard 最经典的例子是旅行商问题的最短路径长度。
我们先来看旅行商问题的决策版本:给定一系列城市和每对城市之间的距离,求解是否存在一个回路,该回路访问每座城市一次并回到起始城市(即哈密顿路径),并且该回路总长度小于 k ?
这个问题是一个 NP 问题:
- 如果有人给你一条路径作为解,你可以在多项式时间内检查它是否是回路、是否经过所有城市,以及它的总长度是否 ≤k
- 我们无法在多项式时间内枚举所有回路,因此不保证能在多项式时间内回答此问题
事实上,这一问题也是 NP-complete 问题,由于证明难度过大,此处不做证明。
在决策版问题的基础上,如果我们将题目要求更改为找出满足该条件的总长度最小的回路,则得到了旅行商问题的优化版。
优化版问题是一个 NP-hard 问题:
- 无法在多项式时间内验证:尽管我们可以验证某个长度的回路存在,但要确定该回路总长度最小,还是需要遍历所有可能性,这在多项式时间内无解
- 决策版问题可以归约为优化版问题:
- 决策版问题的输入是图 G 和整数 k ,优化版问题的输入是图 G
- 决策版问题输出“是”或“否”,优化版问题输出哈密顿路径的最小长度 kmin
- 要解决决策版问题,我们只需要解决优化版问题得到 kmin ,再将 kmin 与 k 比较即可
- 因此,可以通过解决优化版问题来解决决策版本问题。
- 又因为旅行商问题决策版本是 NP-complete 问题,借助 NP-complete 定义,一切 NP 问题都能归约到旅行商问题的优化版本,因此旅行商问题的优化版本是 NP-hard 问题
注
部分内容引用自维基百科。